一、梯度下降法
在机器学习算法中,对于很多监督学习模型,需要对原始的模型构建损失函数l,接下来便是通过优化算法对损失函数l进行优化,以便寻找到最优的参数θ。在求解机器学习参数θ的优化算法中,使用较多的是基于梯度下降的优化算法(Gradient Descent, GD)。
梯度下降法有很多优点,其中,在梯度下降法的求解过程中,只需求解损失函数的一阶导数,计算的代价比较小,这使得梯度下降法能在很多大规模数据集上得到应用。梯度下降法的含义是通过当前点的梯度方向寻找到新的迭代点。
二、梯度下降法的集中变形形式
在具体使用梯度下降法的过程中,主要有以下几种不同的变种,即:batch、mini-batch、SGD和online。其主要区别是不同的变形在训练数据的选择上。
1、batch gradient descent
批梯度下降法(Batch Gradient Descent)针对的是整个数据集,通过对所有的样本的计算来求解梯度的方向。
批梯度下降法的损失函数为:
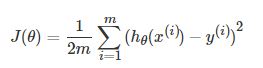
针对上述的损失函数,在批梯度的优化过程中,对每一个样本都需要计算其梯度,批梯度的优化过程为:
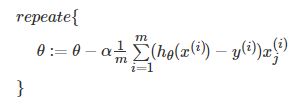
2、mini-batch gradient descent
在上述的批梯度的方式中每次迭代都要使用到所有的样本,对于数据量特别大的情况,如大规模的机器学习应用,每次迭代求解所有样本需要花费大量的计算成本。是否可以在每次的迭代过程中利用部分样本代替所有的样本呢?基于这样的思想,便出现了mini-batch的概念。
假设训练集中的样本的个数为n,则每个mini-batch只是其一个子集,假设,每个mini-batch中含有b个样本,这样,整个训练数据集可以分为n/b个mini-batch。
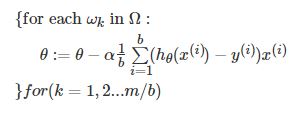
3、stochastic gradient descent
随机梯度下降算法(stochastic gradient descent)可以看成是mini-batch gradient descent的一个特殊的情形,即在随机梯度下降法中每次仅根据一个样本对模型中的参数进行调整,等价于上述的b=1情况下的mini-batch gradient descent,即每个mini-batch中只有一个训练样本。
随机梯度下降法的优化过程为:
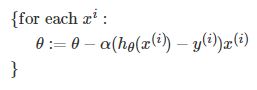
4、online gradient descent
对于互联网上的应用来说,数据的获取变得实时,例如推荐中,系统希望能够根据用户的实时的信息对模型进行调整,这样就产生了在线学习,在线学习(Online Learning)算法就是充分利用实时数据的一个训练算法。
在线梯度下降法(Online gradient descent)对于所有训练数据只用一次,然后丢弃。每次根据实时的数据计算梯度,进而调整模型中的参数。
本文转载自: https://blog.csdn.net/google19890102/article/details/48766869