作者:安平博,Xilinx高级工程师;来源:AI加速微信公众号
卷积占据了CNN网络中绝大部分运算,进行乘法运算通常都是使用FPGA中的DSP,这样算力就受到了器件中DSP资源的限制。比如在zynq7000器件中,DSP资源就较少,神经网络的性能就无法得到提升。利用xilinx器件中LUT的结构特征,设计出的乘法器不但能灵活适应数据位宽,而且能最大限度降低LUT资源使用。
Xilinx ultrascale器件LUT结构
在这里简要介绍一下ultrascale系列器件中的LUT结构,有助于后边对乘法器设计思路的理解。CLB(configuratble logic block)是主要的资源模块,其包含了8个LUT,16个寄存器,carry逻辑,以及多路选通器等。其中LUT可以用作6输入1输出,或者两个5输入LUT,但是这两个LUT公用输入,具有不同输出。每个LUT输出可以连接到寄存器或者锁存器,或者从CLB输出。LUT可以用于64x1和32X2的分布式RAM,一个CLB内最大可以支持512X1大小的RAM。RAM的读写地址和输入的读写数据是共享的,数据通道可以使用x和I接口。LUT还可以配置用于4:1选通器,CLB最大能够支持到32:1的选通器。CLB中的carry逻辑含有异或门和产生进位的门,用于生成进位数据。

图1.1 LUT结构
LUT还可以被动态配置成32bit移位寄存器,这个功能在乘法器设计中可以用于改变乘法器的乘数和被乘数。在写入LUT数据的时候,每个时钟周期从D接口进入数据,依次写入32bit数据。读数据的时候,可以通过地址来定位任何32bit中的数据。这样就可以配置成任何小于32bit的移位寄存器。移位输出Q31可以进入下一级LUT用于串联产生更大移位寄存器。在一个CLB中最大可以串联产生256bit移位寄存器。
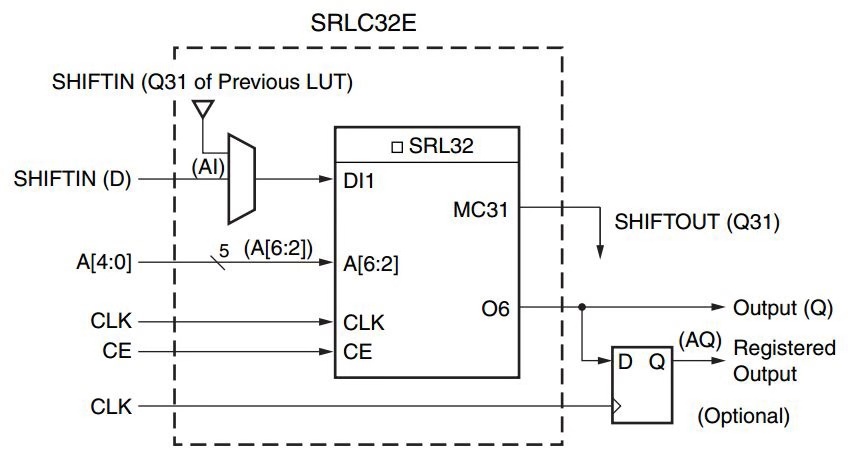
图1.2 移位寄存器配置
LUT乘法器原理
首先假设我们处理整数乘法,小数乘法也可以用这样的方法。基本思想就是将m bit大小的数据进行分割表示:

这样就将两个数据乘法分解成低bit数据乘法,结果是一个常数K和di相乘,然后再进行移位求和。M bit数据分解后的低bit数据位宽通常都适配LUT输入宽度,这样能最大利用LUT资源。现在乘法只有K*di,由于bit位宽较小,这部分可以用LUT查找表的形式来。预先将0K到(2^q-1)K的数据存储到LUT中,然后通过di来选择对应的数据。如果是负数乘法,那么数据使用补码表示,那么LUT中存储的数据是从-2^(q-1)K到(2^(q-1)-1)K。针对以上介绍的ultrascale器件的LUT6,q可以选择为5。但是在本论文中使用的是LUT4器件,其只有4输入,因此选择了q=3,为什么没有选择4呢?另外1bit是为了用于半加器的实现。
基本结构
实现上述累加的方法有很多种,论文中采用了进位链加法器。图2.1中是m bit和n bit数据乘法,每个E结构计算di*K,并且和上一个结构求和,输出的低3bit直接作为最终结果,而n bit传输到下一级进行计算。q=3的计算单元E有[m/3]个。K*di是有n+3bit的查找表实现的。查找表的结果由di选择,然后再通过一个求和器和之前数据求和。这是一个最基本的结构,论文又针对这个结构做了优化,用一个LUT同时实现了一个查找表和半加器。具体来讲,其中3bit输入用于di,还有1bit用于上一次输出,LUT中存放数据是di*K和上一次结果第j bit的半加结果,实际上是第j bit数据LUT中结果的异或。而进位数据由CLB中相应的carry逻辑来计算。相比于粗暴的进行数据求和,这样精确的来控制LUT能够大大节省资源。
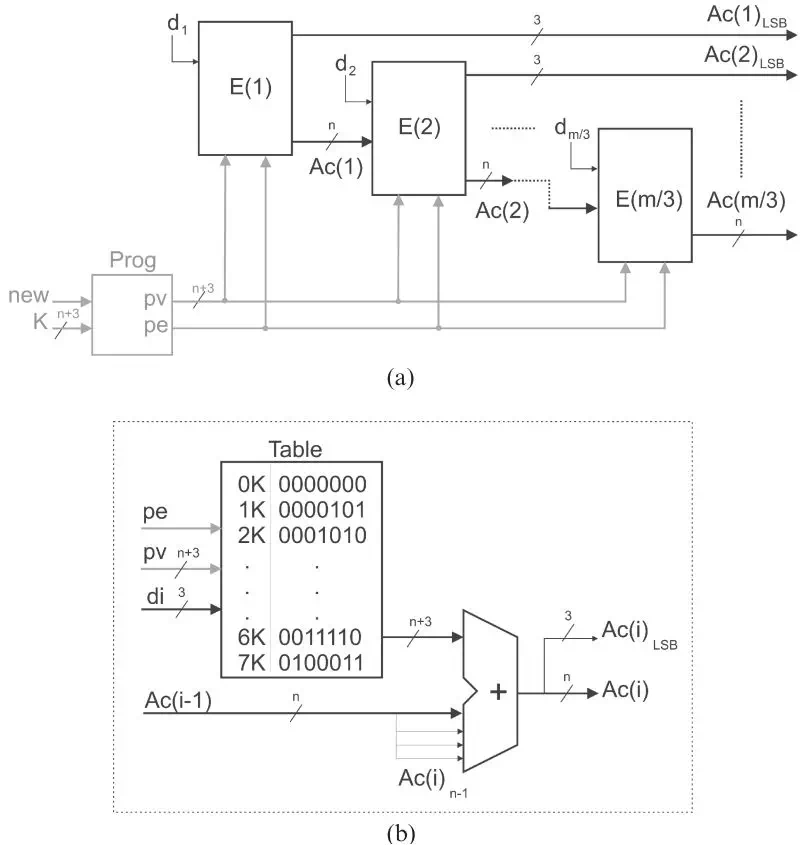
图2.1 基本结构
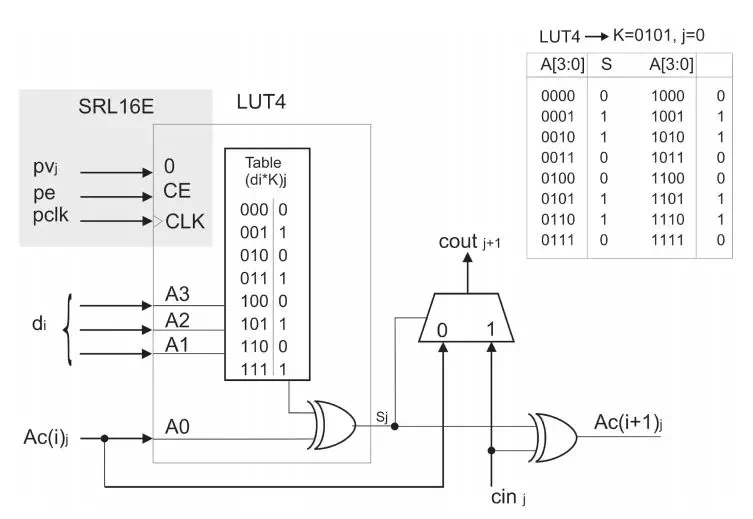
图2.2 LUT实现乘法和半加,外围carry逻辑实现进位
动态配置LUT内容
Xilinx的LUT结构允许在运行过程中改变LUT中的内容,这样的乘法器就能改变被乘数据K。这可以实现在神经网络计算中需要更新权重参数。论文中使用的是LUT4,所以一个LUT可以被配置成16bit移位寄存器。通过这16bit寄存器可以来配置LUT中的内容,每个时钟周期更新1bit数据,16个时钟周期可以完成一个LUT中数据更新。是否进行LUT内容更新通过CE使能信号控制。
如何产生LUT中数据的值呢?如果上一次输出数据对应bit为0,那么LUT中就存放0*K到7*K的值,如果上一次对应bit为1,那么存放值为对以上数据取反。图4.1表示了获得LUT中内容的电路图。首先数据被初始化为0*K,下一次对应着求和进位为1的情况,取反,然后再加K得到1*K的值,这样每隔两个时钟周期就得到下一个乘法的数据值,依次对LUT进行更新。上述中针对的是正整数,如果对于负数乘法更新,可以在上述求整数乘法的电路基础上做一下改进,如图4.2。当最高位为0的时候,输出结果就是之前求得的乘法结果。如果最高位是1,那么负数的补码表示是乘法的原码结果减去最高位数值。

图4.1 LUT中内容更新电路图
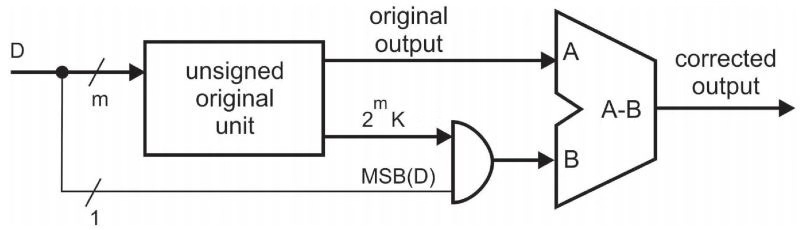
图4.2 负数乘法结果更新电路
结果分析
最后我们来看看这种乘法器的实现效果,图5.1表示对多级进位不适用pipeline结构的时钟频率随着被乘数K位宽变化,可以看到随着级数E的增加,频率降低很多,这主要是进位链边长导致。而随着K位宽增加,频率也有降低,这主要是因为实现di*K乘法的LUT资源增加导致。
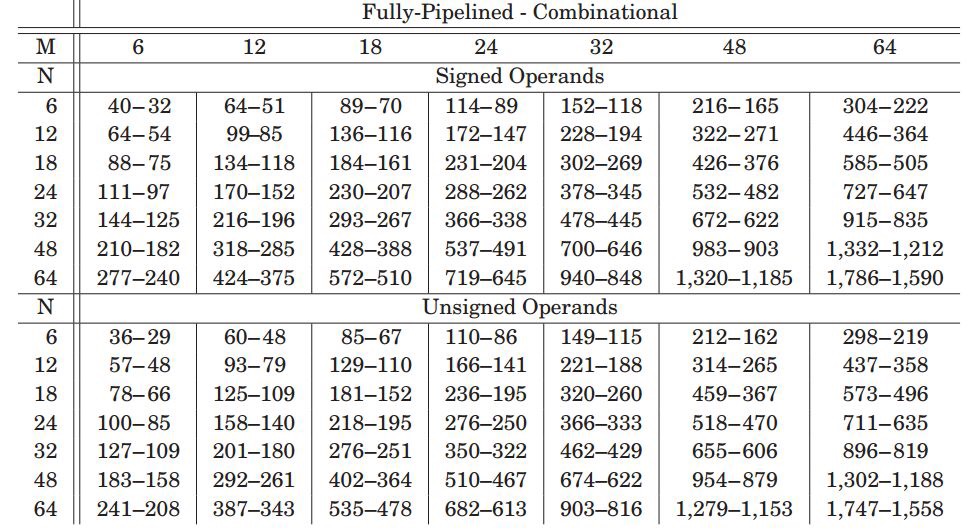
图5.1 没有pipeline下频率MHz
图5.2是不同乘法位宽下的使用slice数量。论文中考虑了两种极端情况,一种是完全pipeline下,即每级计算单元都经过寄存器,另外一种是完全没有pipeline,所有级E都是串联。
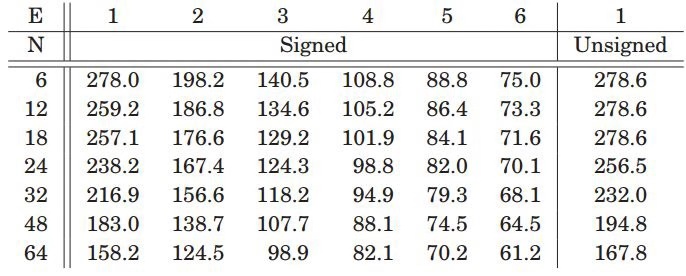
图5.2 slice资源
结论
上述通过LUT来设计乘法器的方法,可以应用于CNN中的卷积运算当中,因为权重可以被当做被乘数,用于LUT内容的配置,在更换权重时,可以对LUT内容更新,这样就能避免了DSP资源的限制,不失为一种增加算力的方法。
文献
1. Hormigo, J.C., Gabriel Oliver, Juan P.Boemo, Eduardo, Self-Reconfigurable Constant Multiplier for FPGA. ACM Transactions on Reconfigurable Technology and Systems, 2013. 6
文章转载自: AI加速





